Authors:
(1) Dorian W. P. Amaral, Department of Physics and Astronomy, Rice University and These authors contributed approximately equally to this work;
(2) Mudit Jain, Department of Physics and Astronomy, Rice University, Theoretical Particle Physics and Cosmology, King’s College London and These authors contributed approximately equally to this work;
(3) Mustafa A. Amin, Department of Physics and Astronomy, Rice University;
(4) Christopher Tunnell, Department of Physics and Astronomy, Rice University.
Table of Links
2 Calculating the Stochastic Wave Vector Dark Matter Signal
3 Statistical Analysis and 3.1 Signal Likelihood
4 Application to Accelerometer Studies
4.1 Recasting Generalised Limits onto B − L Dark Matter
6 Conclusions, Acknowledgments, and References
A Equipartition between Longitudinal and Transverse Modes
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
D The Case of the Gradient of a Scalar
A Equipartition between Longitudinal and Transverse Modes
The equation of motion for the field Ψ (written in Fourier space) is
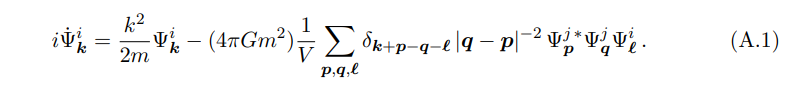
Now, we wish to decompose the field into transverse and longitudinal pieces. Let us call them ηk and ζk. That is,
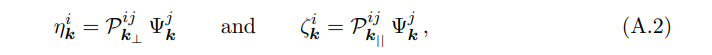
where

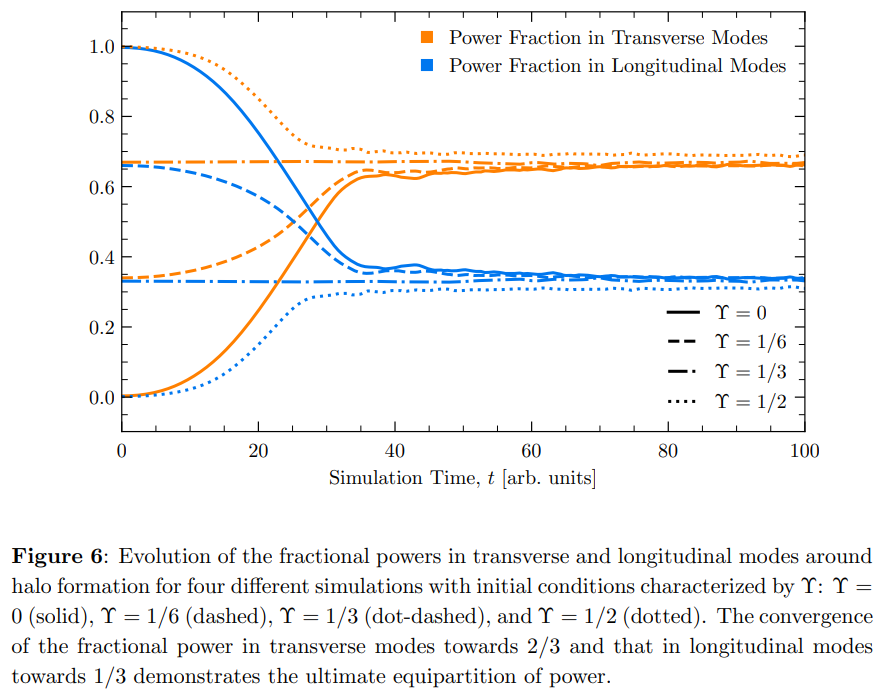
Notice that not only are the longitudinal and transverse pieces coupled to one another, but more importantly they source each other. Hence, we expect virialization between them due to such non-linear gravitational dynamics during DM halo formation, ultimately leading to equipartition of power amongst them. That is, 2/3 of the total power would be in the transverse sector, with the remaining 1/3 in the longitudinal sector.
Using codes based on the split-Fourier technique [73, 91–93], we have performed simulations of the Schrodinger -Poisson vector system [31, 64, 94] (physical space version of Eq. (A.1)):
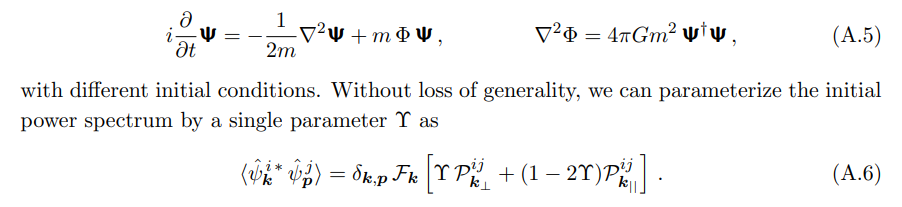

This paper is available on arxiv under CC BY 4.0 DEED license.