Authors:
(1) Dorian W. P. Amaral, Department of Physics and Astronomy, Rice University and These authors contributed approximately equally to this work;
(2) Mudit Jain, Department of Physics and Astronomy, Rice University, Theoretical Particle Physics and Cosmology, King’s College London and These authors contributed approximately equally to this work;
(3) Mustafa A. Amin, Department of Physics and Astronomy, Rice University;
(4) Christopher Tunnell, Department of Physics and Astronomy, Rice University.
Table of Links
2 Calculating the Stochastic Wave Vector Dark Matter Signal
3 Statistical Analysis and 3.1 Signal Likelihood
4 Application to Accelerometer Studies
4.1 Recasting Generalised Limits onto B − L Dark Matter
6 Conclusions, Acknowledgments, and References
A Equipartition between Longitudinal and Transverse Modes
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
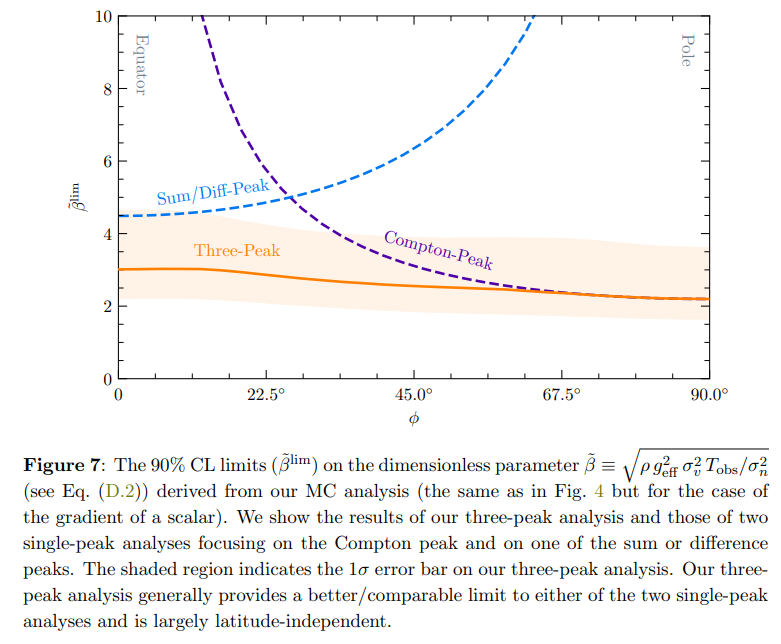
D The Case of the Gradient of a Scalar
C Covariance Matrix
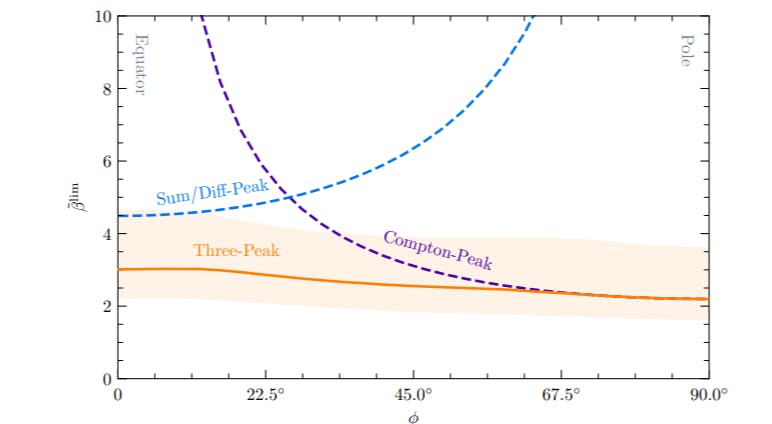
To treat the total likelihood as the product of the individual likelihoods in each frequency bin, we must check that the covariance matrix is diagonal.
We will consider a signal-only analysis, discarding the noise, since the noise merely adds to the power and is uncorrelated between different frequency bins. We may write the values of the three peaks as
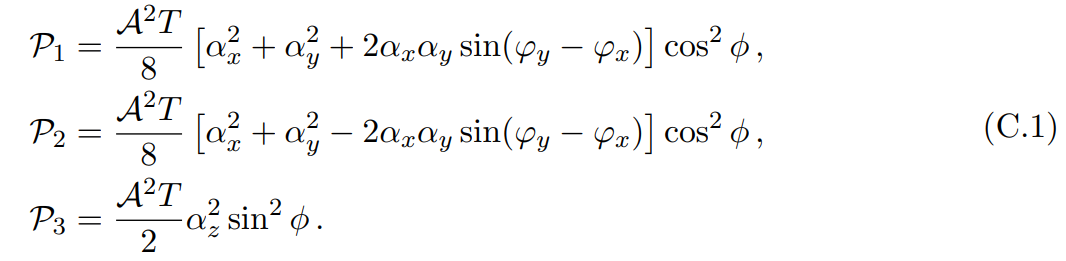
We wish to compute the quantity

We can do this using the expression for the raw moments,
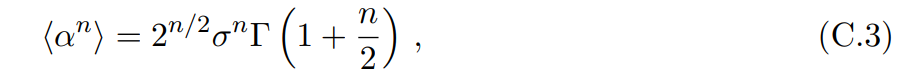
where, for us, σ = 1/ √ 2. Aside from this, we need to know that

We then get that
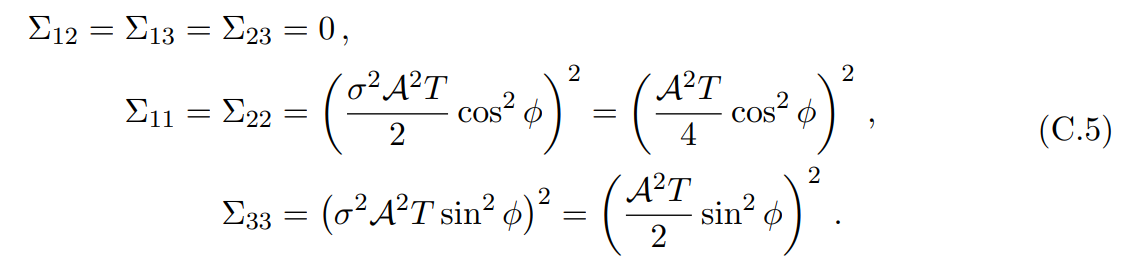
Crucially, we get that the covariance between peaks is 0, allowing us to treat them as statistically independent and hence permitting us to express the total likelihood as the product of the individual likelihoods.
This paper is available on arxiv under CC BY 4.0 DEED license.