Authors:
(1) Antonio Riotto, Département de Physique Theorique, Universite de Geneve, 24 quai Ansermet, CH-1211 Geneve 4, Switzerland and Gravitational Wave Science Center (GWSC), Universite de Geneve, CH-1211 Geneva, Switzerland;
(2) Joe Silk, Institut d’Astrophysique, UMR 7095 CNRS, Sorbonne Universite, 98bis Bd Arago, 75014 Paris, France, Department of Physics and Astronomy, The Johns Hopkins University, Baltimore MD 21218, USA, and Beecroft Institute of Particle Astrophysics and Cosmology, Department of Physics, University of Oxford, Oxford OX1 3RH, UK.
Table of Links
2.1 What is the abundance of PBHs?
2.2 What is the effect of PBH clustering?
2.3 What fraction of the currently observed GW events can be ascribed to PBHs?
3.3 Plugging the pair instability gap with PBH?
3.4 PBH eccentricity, 3.5 PBH spin and 3.6 Future gamma-ray telescopes
2.1 What is the abundance of PBHs?
The formation of a PBH in the early universe is a rare event and knowing the precise formation probability represents, even nowadays, a challenge. This issue is of fundamental importance as the formation probability is one of the key ingredients to calculate the current PBH abundance and mass function which not only enter in many observables, such as the merger rate of BH binaries, but which are also routinely used to express current constraints from various observations.
To illustrate the difficulty in assessing the precise abundance of PBHs, let us consider the most standard scenario in the literature where the PBHs are formed by the collapse of large inhomogeneities generated during the inflationary stage. The latter delivers a stochastic quantity, the curvature perturbation ζ on super horizon scales, whose properties are known statistically. As we mentioned, PBHs are rare events which require a given observable, e.g. the density contrast δ or the compaction function C, to be above a typically large critical value. This implies that the calculation of the PBH abundance requires going beyond linear perturbation theory and the knowledge of the tail of the probability where the latter is typically far from being a simple Gaussian distribution. Nonlinearities enter into the game even when the initial curvature perturbation is Gaussian (which is typically not) because of the nonlinear relation between the over density/compaction function an the curvature perturbation itself. The logic chain is (in radiation)

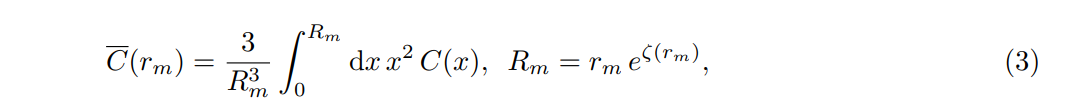
but no calculation exists in the literature so far and no understanding of why the volume average of the compaction function has a critical threshold which does not depend on the profile. Even without the need of mentioning other possible problems, e.g. dealing with the nonlinearities entering in the radiation transfer function when perturbations re-enter the horizon [3] or the need to deal with the phenomenon of operator mixing [4], we believe the calculation of the PBH abundance in the standard scenario is still an open issue which deserves further study. The same is true in alternative mechanisms to generate the PBHs, e.g. in supercooled first-order phase transitions [5] where the threshold criterion does not suffice.
This paper is available on arxiv under CC BY 4.0 DEED license.

